
We here provide excerpts from Jackson's book, Classical Electrodynamics, 3rd edition, John Wiley & Sons, 1999, and comments that illustrate one of the problems with Maxwell's electrodynamics considered as a system of mathematical equations. The problem is that the symbol that Jackson assigns to "Coulomb's law" is also used for the electrodynamic field. These are not the same thing, as shown below. This leads to contradictions, and to the inability to mathematically verify Gauss's law as it appears in Maxwell's system of equations for electrodynamics.
Note that in Jackson's book Classical Electrodynamics, 3rd ed., Gauss's Law is derived in Chapter I "Introduction To Electrostatics," on pages pp. 27 - 31.

This is defining what Jackson means by the symbol \( \mathbf{E} \) (bold face are Jackson's vectors). This definition of \( \mathbf{E} \) is also called the Coulomb field by some authors.
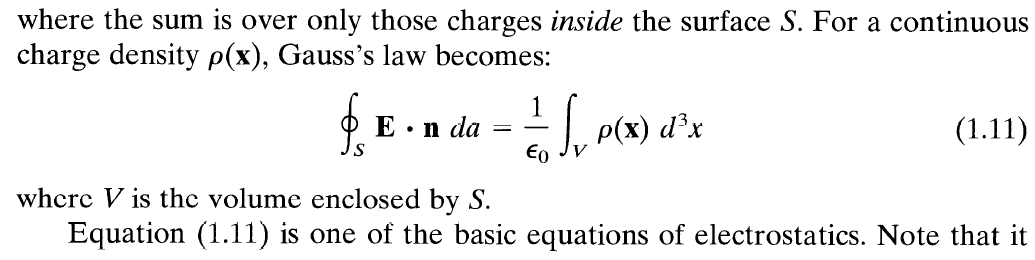
This provides Gauss's law in integral form. Note that Gauss's Law is derived for electrostatics, not electrodynamics. Yet it ends up being one of the four equations of Maxwell's electrodynamics.

Jackson here has written Gauss's Law in differential form, and calls it "Gauss's law of electrostatics". As written, this appears exactly the same (same symbols) as in Maxwell's equations of electrodynamics.
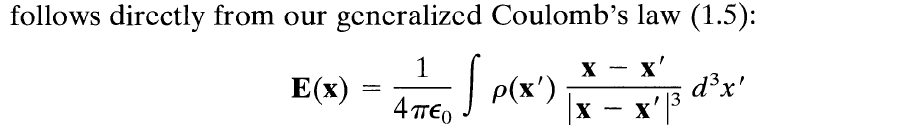
Jackson here calls his Eq. (1.5) "Coulomb's law". We, and some others, call it the "Coulomb field".
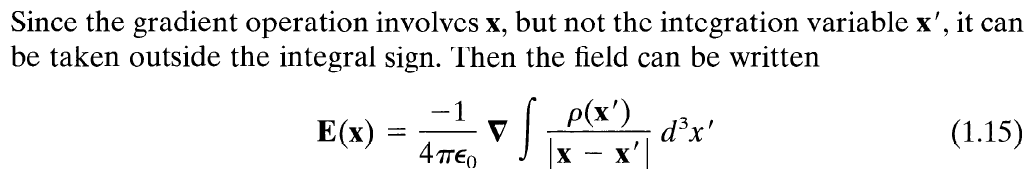

This shows the connection of Gauss's Law, in differential form, written as Jackson's Eq. (1.13), and the scalar potential function of Jackson's Eq. (1.17).
Clearly, Gauss's Law is derived for the Coulomb field (Jackson's Eq. (1.5), although Jackson does not call this the Coulomb field, other authors do) and is not here derived for the more general electrodynamics field.
So, in Maxwell's equations, where Gauss's Law is given as one of the four differential equations, it is the Coulomb field, not the general electrodynamic field, that is to be used. And this has been mathematically verified by performing the indicated differentiation on the left-hand side of the equation to find that only the Coulomb field is mathematically consistent with Gauss's Law.
Why shouldn't this be the case? After all, Jackson has only derived Gauss's Law in his chapter on electrostatics.
Jackson makes the mistake, as other authors have, of using the same symbol for Coulomb's law (his Eq. (1.5), or Eq. (1.16) in scalar potential form) and the more general electrodynamic field. Since these are clearly different concepts, different notation is required for these two concepts, regardless of whether or not one is "simply a special case of the other."
Note that later in the book, in the Chapter "Maxwell Equations, Macroscopic Electromagnetism, Conservation Laws", Jackson writes, p. 239
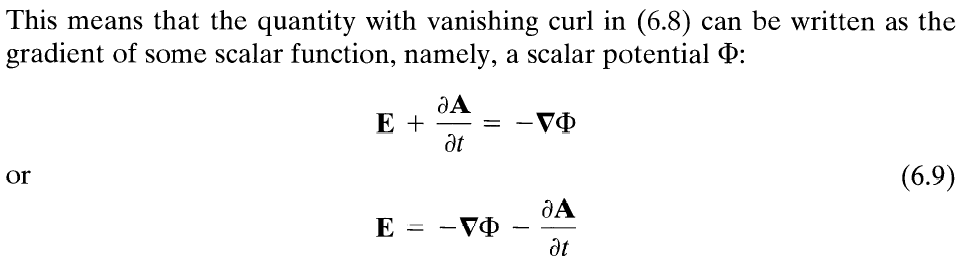
But we just saw that Jackson uses (Jackson's Eq. (1.16) above) $$ \mathbf{E} = - \nabla \Phi . $$
This, Jackson's Eq. (6.9), is a mistake in notation. Since \( -\nabla \Phi \) is already assigned the symbol \( \mathbf{E} \) we must use another symbol for \( -\nabla \Phi -\partial \mathbf{A} / \partial t .\) We prefer to change the notation for the Coulomb field (Jackson's Coulomb law, Eq. (1.16)) to be $$ \mathbf{E}^{(C)} = -\nabla \Phi $$ so that we can use the symbol \( \mathbf{E} \) for $$ \mathbf{E} = -\nabla \Phi - \dfrac{\partial}{\partial t} \mathbf{A} = \mathbf{E}^{(C)} - \dfrac{\partial}{\partial t} \mathbf{A}. $$
This notational change clarifies the situation and does not lead to any contradictions, as Jackson's (and other's) original notation does. This makes Gauss's Law simple, clear, and mathematically verifiable.
On p. 241, Jackson writes
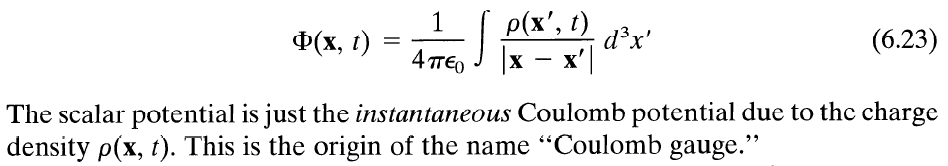
Here, Jackson defines the scalar potential function, as he has previously, but now with a time varying charge density function. So we know Jackson intends the scalar potential function to be the same as his scalar potential function in the electrostatic case, but now with the time constrant of electrostatics lifted.
This website is Copyright © 2018. All rights reserved.
Contact email: WeberElectrodynamics(AT)gmail.com